几种常用loss函数原理及代码示例

No tag
Publish Date:   2024-09-18
Update Date:   2024-10-15
Word Count:   1.7k
Read Times:   8 Min
Read Count:  

0.信息熵

  • 计算公式

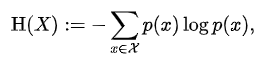
  • 说明

Onehot向量的信息熵为0

非Onehot向量的概率分布反而有一定的信息熵

对于交叉熵而言，与Onehot向量相同的概率分布时，其交叉熵也为0

1.交叉熵损失 Cross Entropy Loss (CE loss)

  • 计算公式：

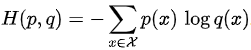
  • 公式实际应用说明:

    其中p(x)代表了标签(或者每个标签的概率)，q(x)代表了模型预测的概率

  • 代码示例

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, NC]
batchsize = 2
num_class = 4

# 神经网络的输出值，没有经过softmax，未归一化
logits = torch.randn(batchsize, num_class)
# delta 目标分布
hard_label = torch.randint(num_class, size=(batchsize,))
# 非 delta 目标分布
soft_label = torch.randn(batchsize, num_class)


### method 1 for CE loss
### hard label，常用在分类之中
ce_loss_fun = torch.nn.CrossEntropyLoss()
ce_loss = ce_loss_fun(logits, hard_label)
print(f"cross entropy loss1: {ce_loss}")

### method 2 for CE loss
### soft label，常用在知识蒸馏中
ce_loss = ce_loss_fun(logits, torch.softmax(soft_label, -1))
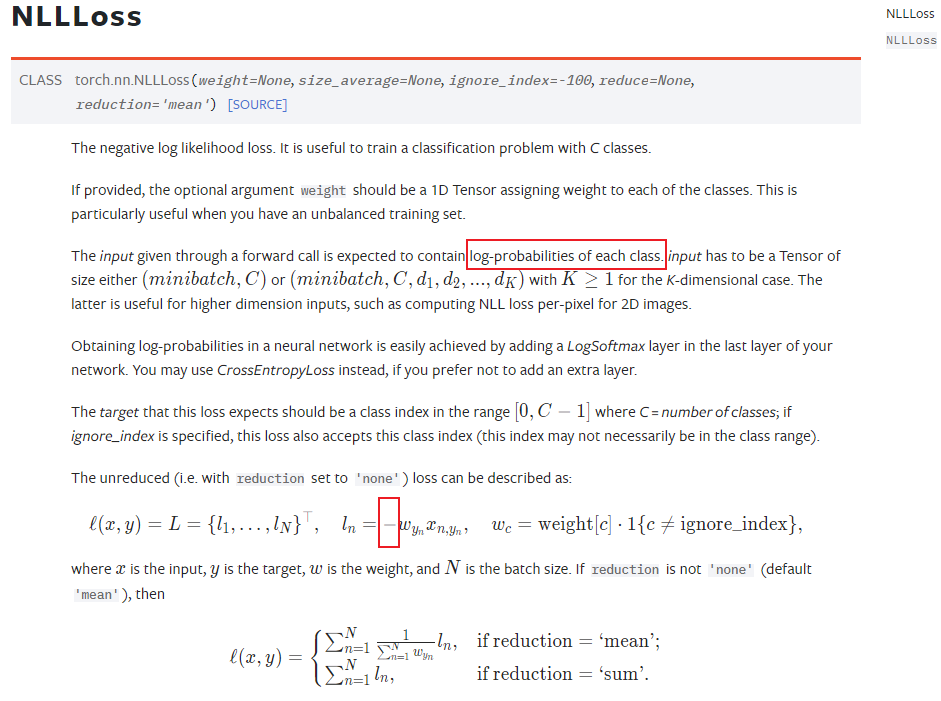
print(f"cross entropy loss2: {ce_loss}")

2.负对数似然损失 Negative Log Likelihood Loss (NLL loss)

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, NC]
batchsize = 2
num_class = 4

# 神经网络的输出值，没有经过softmax，未归一化
logits = torch.randn(batchsize, num_class)
# delta 目标分布
hard_label = torch.randint(num_class, size=(batchsize,))

nll_fn = torch.nn.NLLLoss()
nll_loss = nll_fn(torch.log(torch.softmax(logits, dim=-1)), hard_label)  # 与 CE loss结果相同
print(f"negative log-likelihood loss: {nll_loss}")
### cross entropy value = NLL value

这里注意到：cross entropy value = NLL value
也就是说，能用CE loss的地方，就能用NLL loss
取决于输出的是什么，分两种情况：

  • 神经网络输出的是未归一化的分数的话：那么就用CE loss
  • 神经网络输出的是一个概率值，甚至是一个对数概率值的话：那么就用NLL loss

总之他们俩是殊途同归的

  • 对数似然，就是负的交叉熵
  • 交叉熵，就是负对数似然

3.Kullback-Leibler divergence loss（KL loss）

反映的是：预测分布和目标分布之间的距离度量

计算公式如下：

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, NC]
batchsize = 2
num_class = 4

logits = torch.randn(batchsize, num_class)
soft_label = torch.randn(batchsize, num_class)  # delta 目标分布

kld_loss_fn = torch.nn.KLDivLoss()
kld_loss = kld_loss_fn(torch.log(torch.softmax(logits, dim=-1)), torch.softmax(soft_label , dim=-1))
print(f'Kullback-Leibler divergence loss:{kld_loss}')

4.验证 CE = IE + KLD

即：交叉熵 = 信息熵 + KLD散度

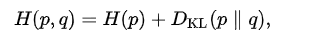
其中p(x)代表了真实分布，q(x)代表了预测分布

代码验证

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, NC]
batchsize = 2
num_class = 4

# 神经网络的输出值，没有经过softmax，未归一化
logits = torch.randn(batchsize, num_class)
# delta 目标分布
hard_label = torch.randint(num_class, size=(batchsize,))
# 非 delta 目标分布
soft_label = torch.randn(batchsize, num_class)


ce_loss_fn_sample = torch.nn.CrossEntropyLoss(reduction="none")
ce_loss_sample = ce_loss_fn_sample(logits, torch.softmax(soft_label, dim=-1))
print(f"cross entropy loss sample: {ce_loss_sample}")

kld_loss_fn_sample = torch.nn.KLDivLoss(reduction="none")
kld_loss_sample = kld_loss_fn_sample(torch.log(torch.softmax(logits, dim=-1)), torch.softmax(soft_label, dim=-1)).sum(-1)
print(f'Kullback-Leibler divergence loss sample:{kld_loss_sample}')

target_information_entropy = torch.distributions.Categorical(probs=torch.softmax(soft_label, dim=-1)).entropy()
print(f'information entropy sample:{target_information_entropy}')  # IE为常数，如果目标分布是delta分布，IE=0

print(torch.allclose(ce_loss_sample, kld_loss_sample+target_information_entropy))

对于delta分布，即对于onehot变量，信息熵是一个0，0对于卷积神经网络的参数更新时没有任何贡献的，此时，优化CE_loss与优化KLD_loss是没有任何区别，效果是一样的

对于非delta分布，即对于非onehot变量，信息熵是一个常数，常数对于卷积神经网络的参数更新时没有任何贡献的，此时，优化CE_loss与优化KLD_loss是没有任何区别，效果是一样的

5.Binary Cross Entropy loss（BCE loss）

对判别器输出是真还是假，就属于二分类问题了

代码示例

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, 1]

bce_loss_fn = torch.nn.BCELoss()
nll_fn = torch.nn.NLLLoss()

batchsize = 2
logits = torch.randn(batchsize)
prob_1 = torch.sigmoid(logits)
target = torch.randint(2, size=(batchsize, ))
bce_loss = bce_loss_fn(prob_1, target.float())
print(f"binart cross entropy loss: {bce_loss}")

### 用NLL loss代替BCE loss做二分类
prob_0 = 1-prob_1.unsqueeze(-1)
prob = torch.cat([prob_0, prob_1.unsqueeze(-1)], dim=-1)
nll_loss_binary = nll_fn(torch.log(prob), target)
print(f"negative likelihood loss binary: {nll_loss_binary}")
print(torch.allclose(bce_loss, nll_loss_binary))

本质上，都是2个概率分布的映射
sigmoid 的作用是将输出值转换为0-1之间的浮点型
如果不想添加sigmoid函数的话，那么就直接用BCEWithLogitsLoss函数，如下图

但是，在BCE loss函数中，当输入数值变大的情况下，容易出现为0的情况，如下代码及结果所示：

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
logits = torch.linspace(-10, 10, 2000)
loss = []
loss_fn = nn.BCELoss()
for lgs in logits:
    loss.append(loss_fn(torch.sigmoid(lgs), torch.ones_like(lgs)))
plt.plot(logits, loss)
plt.show()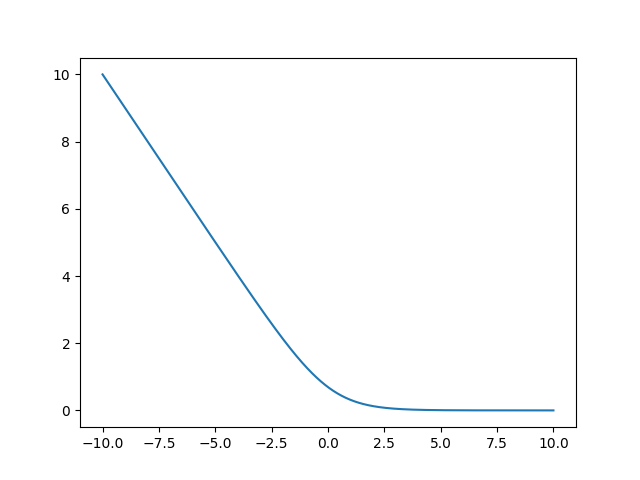

6.Cosine Similarity loss

数学表达式

import torch
import torch.nn as nn
import torch.nn.functional as F

batchsize = 2

cosine_loss_fn = torch.nn.CosineEmbeddingLoss()

#生成具有正态分布（均值为0，标准差为1）的随机数的函数
v1 = torch.randn(batchsize, 512)
v2 = torch.randn(batchsize, 512)
# target只能是0或者1
# 因此：0~1 -> 0~2 -> -1~1
target = torch.randint(2, size=(batchsize, ))*2-1
cosine_loss = cosine_loss_fn(v1, v2, target)
print(f"cosine similarity loss: {cosine_loss}")

应用领域

  • 自监督学习
  • 对比学习
  • 相似度匹配
  • 文本检索
  • 图像检索

7.前述分类损失函数测试代码汇总

import torch
import torch.nn as nn
import torch.nn.functional as F

# logits shape: [BS, NC]
batchsize = 2
num_class = 4

logits = torch.randn(batchsize, num_class)
target_indices = torch.randint(num_class, size=(batchsize,))  # delta 目标分布
target_logits = torch.randn(batchsize, num_class)  # 非 delta 目标分布

# 1. 交叉熵损失 Cross Entropy Loss (CE loss)
print("----------------------------------------------------------")
## 1. 调用 Cross Entropy loss

### method 1 for CE loss
ce_loss_fun = torch.nn.CrossEntropyLoss()
ce_loss = ce_loss_fun(logits, target_indices)
print(f"cross entropy loss1: {ce_loss}")

### method 2 for CE loss
ce_loss = ce_loss_fun(logits, torch.softmax(target_logits, -1))
print(f"cross entropy loss2: {ce_loss}")

# 2.负对数似然损失 Negative Log Likelihood Loss (NLL loss)
print("----------------------------------------------------------")

nll_fn = torch.nn.NLLLoss()
nll_loss = nll_fn(torch.log(torch.softmax(logits, dim=-1)), target_indices)  # 与 CE loss结果相同
print(f"negative log-likelihood loss: {nll_loss}")
### cross entropy value = NLL value

# 3. 调用 Kullback-Leibler divergence loss（KL loss）
print("----------------------------------------------------------")

kld_loss_fn = torch.nn.KLDivLoss()
kld_loss = kld_loss_fn(torch.log(torch.softmax(logits, dim=-1)), torch.softmax(target_logits, dim=-1))
print(f'Kullback-Leibler divergence loss:{kld_loss}')

# 4.验证 CE = IE + KLD
print("----------------------------------------------------------")

ce_loss_fn_sample = torch.nn.CrossEntropyLoss(reduction="none")
ce_loss_sample = ce_loss_fn_sample(logits, torch.softmax(target_logits, dim=-1))
print(f"cross entropy loss sample: {ce_loss_sample}")

kld_loss_fn_sample = torch.nn.KLDivLoss(reduction="none")
kld_loss_sample = kld_loss_fn_sample(torch.log(torch.softmax(logits, dim=-1)), torch.softmax(target_logits, dim=-1)).sum(-1)
print(f'Kullback-Leibler divergence loss sample:{kld_loss_sample}')

target_information_entropy = torch.distributions.Categorical(probs=torch.softmax(target_logits, dim=-1)).entropy()
print(f'information entropy sample:{target_information_entropy}')  # IE为常数，如果目标分布是delta分布，IE=0

print(torch.allclose(ce_loss_sample, kld_loss_sample+target_information_entropy))

# 5.Binary Cross Entropy loss（BCE loss）
print("----------------------------------------------------------")

bce_loss_fn = torch.nn.BCELoss()
logits = torch.randn(batchsize)
prob_1 = torch.sigmoid(logits)
target = torch.randint(2, size=(batchsize, ))
bce_loss = bce_loss_fn(prob_1, target.float())
print(f"binart cross entropy loss: {bce_loss}")

### 用NLL loss代替BCE loss做二分类
prob_0 = 1-prob_1.unsqueeze(-1)
prob = torch.cat([prob_0, prob_1.unsqueeze(-1)], dim=-1)
nll_loss_binary = nll_fn(torch.log(prob), target)
print(f"negative likelihood loss binary: {nll_loss_binary}")
print(torch.allclose(bce_loss, nll_loss_binary))

# 6.调用 Cosine Similarity loss
print("----------------------------------------------------------")

cosine_loss_fn = torch.nn.CosineEmbeddingLoss()
v1 = torch.randn(batchsize, 512)
v2 = torch.randn(batchsize, 512)
target = torch.randint(2, size=(batchsize, ))*2-1
cosine_loss = cosine_loss_fn(v1, v2, target)
print(f"cosine similarity loss: {cosine_loss}")

运行结果

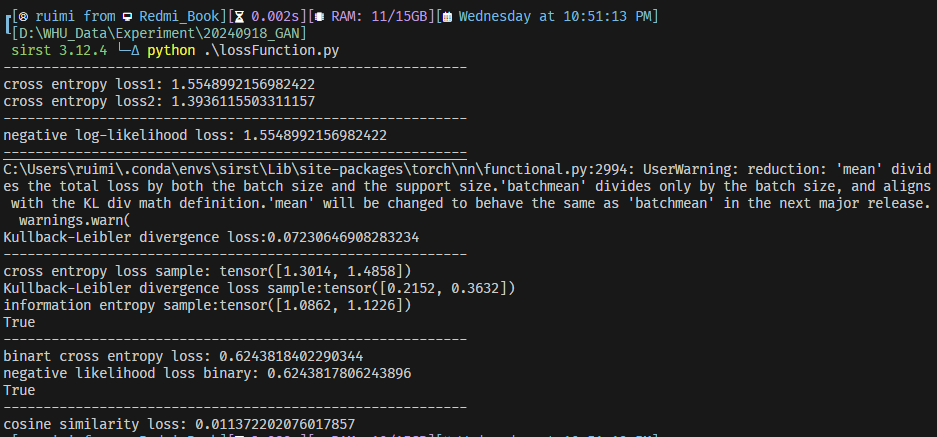
  • 分类的损失函数，本质上是2个概率分布的比较

8.L1loss

  • 也被成为MAE
  • 基本不用在分类中

9.MSEloss

  • 即为MSE
  • 基本不用在分类中

Author: Ruimin Huang
Link: http://www.huangruimin.tech/2024/09/18/ji-chong-chang-yong-loss-han-shu-yuan-li-ji-dai-ma-shi-li/
Reprint policy: All articles in this blog are used except for special statements CC BY 4.0 reprint polocy. If reproduced, please indicate source Ruimin Huang !
No tag
赏
  TOC